What Is The Formula For Radius Of A Circle

Move the loose number over to the other side. Group the x-stuff and y-stuff together. Divide off by whatever is multiplied on the squared terms.

Take the coefficient on the x-term, multiply by one-half, square, and add inside the x-stuff and also to the other side. Convert the left-hand side to squared form, and simplify the right-hand side. If necessary, fiddle with signs and exponents to make your equation match the circle equation's format. The center is at ( 1/2, – 6/5 ) and the radius is 3/2. Technically you can't "calculate" the radius in such a situation. However, it is possible, by construction, to locate the center of such a circle, and then, simply by physically measuring, determine the radius.

To do the construction, draw any two chords and construct their perpendicular bisectors; their point of intersection is the center of the circle. Then draw in any radius and measure it with a ruler. Not technically a "calculation."

Calculator techniques for problems related to circles and triangles are more on algebra, trigonometry, and geometry. Memorization of formulas is what is needed. Here are the contents of the article. The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference.

The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. The radius is half of this distance. You can also think of the radius as the distance between the center of the circle and its edge. In this lesson we'll look at how to write the equation of a circle in standard form in order to find the center and radius of the circle.

An arc is a part of the circumference of the circle. It is part of a curve of a circle. A chord is the line segment drawn by the two different points on the circle.

It is a straight line with both endpoints on the circle. The diameter is the longest chord of a circle that passes through the centre of the circle. A sector is the portion of the circle formed by two radii of the circle and a sector helps in finding the length of the arc.

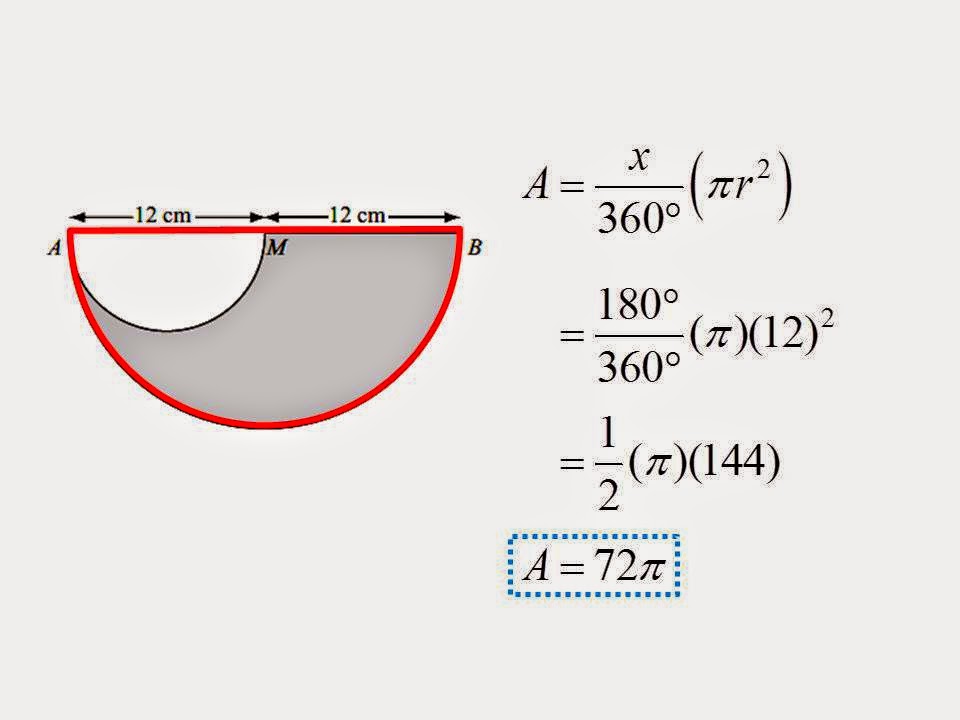
The height of the circular segment becomes one of the segments of the second imaginary cord. We can solve the second segment by dividing the square of the given two segments by the height of the circular segment. The height of the circular segment is one of the segments of our imaginary created cord. If we add them both together they create the diameter length of the circle. Sometimes in order to write the equation of a circle in standard form, you'll need to complete the square twice, once for x and once for y.

Sometimes in order to write the equation of a circle in standard form, you'll need to complete the square twice, once for ??? If the diameter of a circle is known then the formula for radius is diameter divided by 2. If the circumference of a circle is known then the formula for radius is the circumference divided by 2 pi. And if the area of a circle is known then the formula for radius is the square root of the area divided by pi. Write the formula for circumference of circle with radius r. A circle is the set of points in a plane that are equidistant from a given point .

The distance from the centeris called the radius, and the point is called the center. Twice the radius is known as the diameter . The angle a circle subtends from its center is a full angle, equal to or radians. The inner line segments of the sector both equal the radius of the circle. The angle that these two measurements make is called a central angle.

Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions. Diameter Diameter is the measure of the distance across the center of a circle.

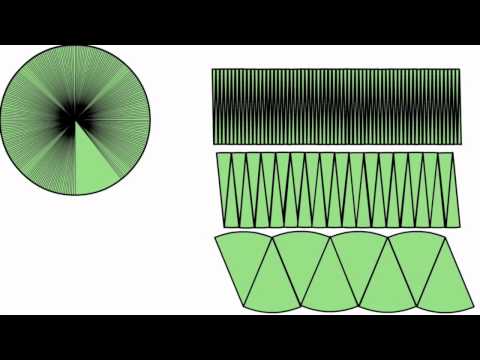
The diameter is equal to twice the measure of the radius. Let us again imagine that a full pizza is divided into 8 equal sizes. Now let's rearrange the pieces in the form of a rectangle. Now the base of the rectangle is the radius and the height is the half of circumference. Because both sides together make up the circle. So height becomes πr since circumference is 2πr.

The circumference is the boundary enclosing the area within it. If an object does not have a center, the term may refer to its circumradius, the radius of its circumscribed circle or circumscribed sphere. In either case, the radius may be more than half the diameter, which is usually defined as the maximum distance between any two points of the figure.

The inradius of a geometric figure is usually the radius of the largest circle or sphere contained in it. The inner radius of a ring, tube or other hollow object is the radius of its cavity. The distance around a rectangle or a square is as you might remember called the perimeter.

The distance around a circle on the other hand is called the circumference . Radius formula is simply derived by halving the diameter of the circle. When we connect a point on the circumference of a circle to the exact centre, then the line segment made is called the radius of the ring. The distance between the center of the circle to its circumference is the radius. The diameter is always double the radius. Hence, the formula is derived by dividing the diameter by 2.

To calculate the radius of a circle by using the circumference, take the circumference of the circle and divide it by 2 times π. For a circle with a circumference of 15, you would divide 15 by 2 times 3.14 and round the decimal point to your answer of approximately 2.39. Be sure to include the units in your answer. The area of ​​a circle refers to the measure of the surface bounded by a circumference. And it is calculated as the product of the radius times the radius times 3.14.

On a piece of paper, draw a circle with a radius of 5 cm. The radius is half the diameter. The area of the triangle inscribed in a circle is 39.19 square centimeters, and the radius of the circumscribed circle is 7.14 centimeters.

If the two sides of the inscribed triangle are 8 centimeters and 10 centimeters respectively, find the 3rd side. According to classical geometry, the radius of a circle is defined as the equal distance drawn from the centre to the circumference of the circle. If we double this distance, then it becomes the diameter of the circle. When you move around with respect to a specific point, then it forms a circle, only if you move in the fixed path. The point which you are taking as your references is called the centre of the circle. The path you follow while moving around forms the circumference of the circle.

The distance that remains fixed while moving about a point is called the radius of a circle. Working with circles has always been very interesting. It is an important part of the mathematics concept to study. Once again in this example, we're given the radius of the circle.

Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m.

At this point we will be creating a perfect square trinomial for the x terms as well as the y terms. Recall that a perfect square trinomial is of the formand it factors in the form. When it is in that form it will allow us to continue onto the next step and write the equation in standard form,.

Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? Use 3.14 as an approximation for pi.

Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference. You can also calculate the circumference of a circle with a given radius by using algebra to isolate the C in our formula. The area of a circle is equal to pi times the radius squared.

Divide the central angle into 360°. Multiply the resulting number by the arc length. That gives you the circumference of the circle. Half of the diameter is the radius of the circle. It is possible to have quite a few circles, all with different radii, in which one could draw a chord of a given, fixed length.

Hence, the chord length by itself cannot determine the radius of the circle. A Circle is defined as a closed figure as the other geometrical shapes and figures. But, as we know, a Circle consists of an inside as well as an outside area like other geometric shapes.

In a circle, however, there is no such property. It does not form any angle or a straight line. In a circle, it is defined as a closed figure as other geometrical shapes and figures. However, the statement itself is contradictory.

A circle has an inside and an outside area just like other geometric shapes. However, it is contradictory in the fact that other shapes and figures like square, rectangle, triangle, and trapezium have some angles or straight sides. However, there are no such conditions in the case of the circle.

It does not form any angle or the straight line. Thus the statement and definition of the circle are itself contradictory to the properties of a closed figure. An arc is the part of the circumference of the circle. It is the curved part of the circle. However, a chord will be the line segment drawn by the two different points on the circle.

A sector helps in finding the length of the arc. Calculate angle measures using both the circumference formula and the arc length theorem. This step isn't really part of finding the center or the radius. But in some cases you will need to graph your circle after finding those two items.

You can graph your circle by plotting your center and then using your radius to find points on the circle. All points on the circle are a fixed distance away from the center . If your equation is in standard form it will make it easier for you to identify the center and radius. Finding the radius of a circle requires you to use formulas such as the area or sector area of a circle formulas. You can also use the diameter and the circumference to find the missing length of a radius. The circle above displays circumference and diameter.